multi-modal-imputation-spatial-gene-expression

Imputation of Spatial Gene Expression with a Multi Modality Deep Learning Network

Final project submission for MSC in Machine Learning / Data Science, Reichman University.

Submitted by: Itay Ben Shushan.

Supervised by: Leon Anavy.

Brief Background

Spatial RNA Sequencing is a recent advance in RNA sequencing, which performs a similar process as single-cell RNA sequencing (scRNA-Seq), while also maintaining the original position of the cell in the tissue. The output of Spatial RNA Sequencing is a matrix, where each column represents a single gene, each row represents a single spot in the tissue, and the value of each cell represents the number of copies found - of a specific gene in a specific spot. Each of the spots then also has extra positional metadata relative to the tissue.

In some databases, the output of the Spatial RNA-seq also includes a high resolution image of the analyzed slice after it underwent histological staining. Each spot is then associated with a specific X,Y pixel coordinates on the image.

The image below shows a sample slice on the left, and the spot positions outlined on top of the slice on the right.

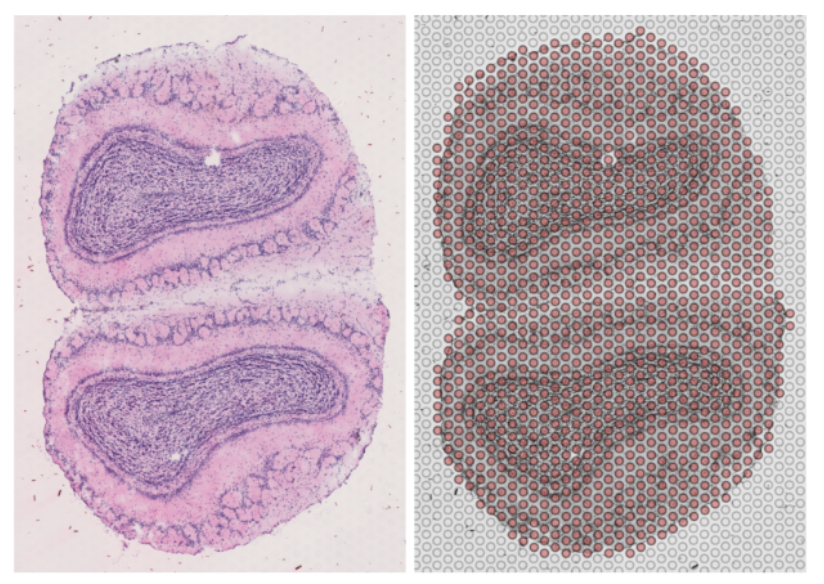
Due to restrictions of the methods in both scRNA-Seq and Spatial RNA-Seq (which stem from having a very small cell-count for the sequencing process) the output matrix contains a significant amount of zeros which don’t always indicate biologically-true absence of expression, but rather some are a cause of methodological noise. This sparsity imposes difficulties on downstream analysis’ of the sequencing data, and performing some form of imputation on single cell transcription data is a frequent practice.

Goal

The goal of this work is to utilize information available in Spatial RNA Sequencing to perform imputation of the gene-count matrix. Specifically, we intend to utilize three modalities to perform an imputed reconstruction of the gene-count matrix:

• The gene-count matrix itself.
• Positional information of each spot - Each spot has an associated X,Y coordinate within the image.
• Image information of each spot. We can extract, from the original high resolution slice image, a small image (tile) around each spot and use its pixel data.

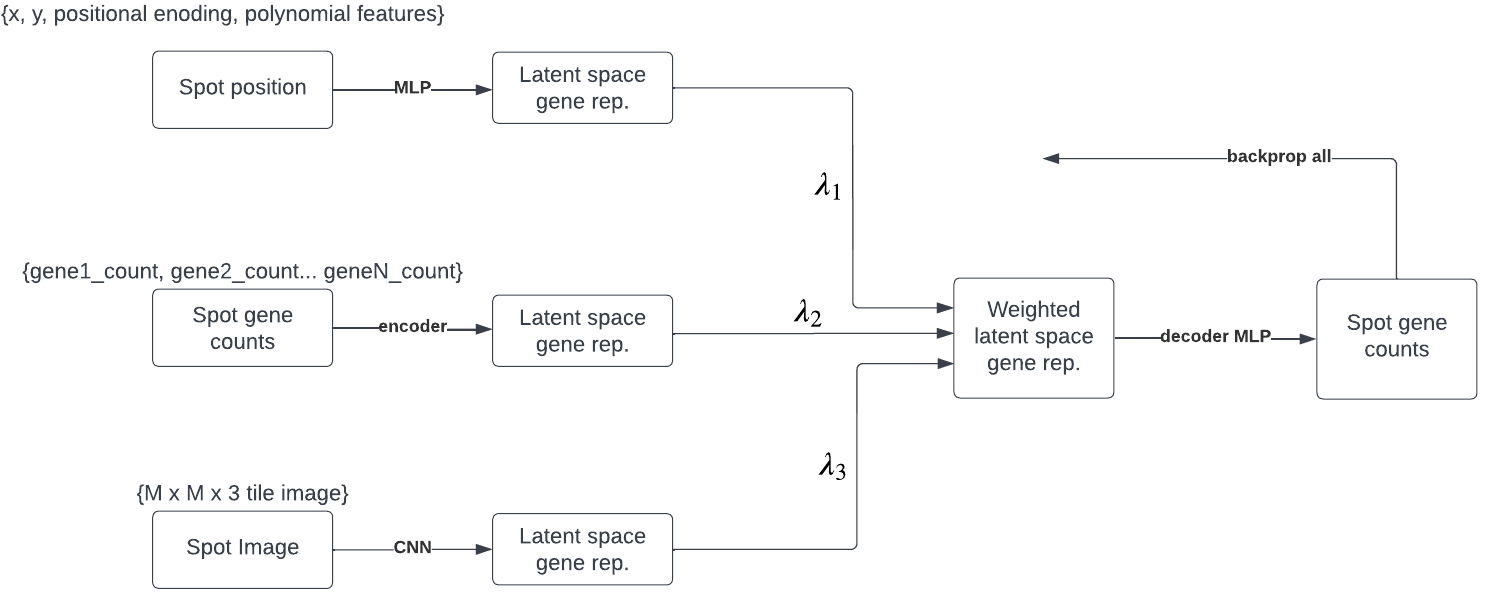
In this work we experiment with imputation in each one of the above approaches individually, and then present a network which uses all modalities in a unified architecture. This final architecture is outlined in the figure below.

Results - summary

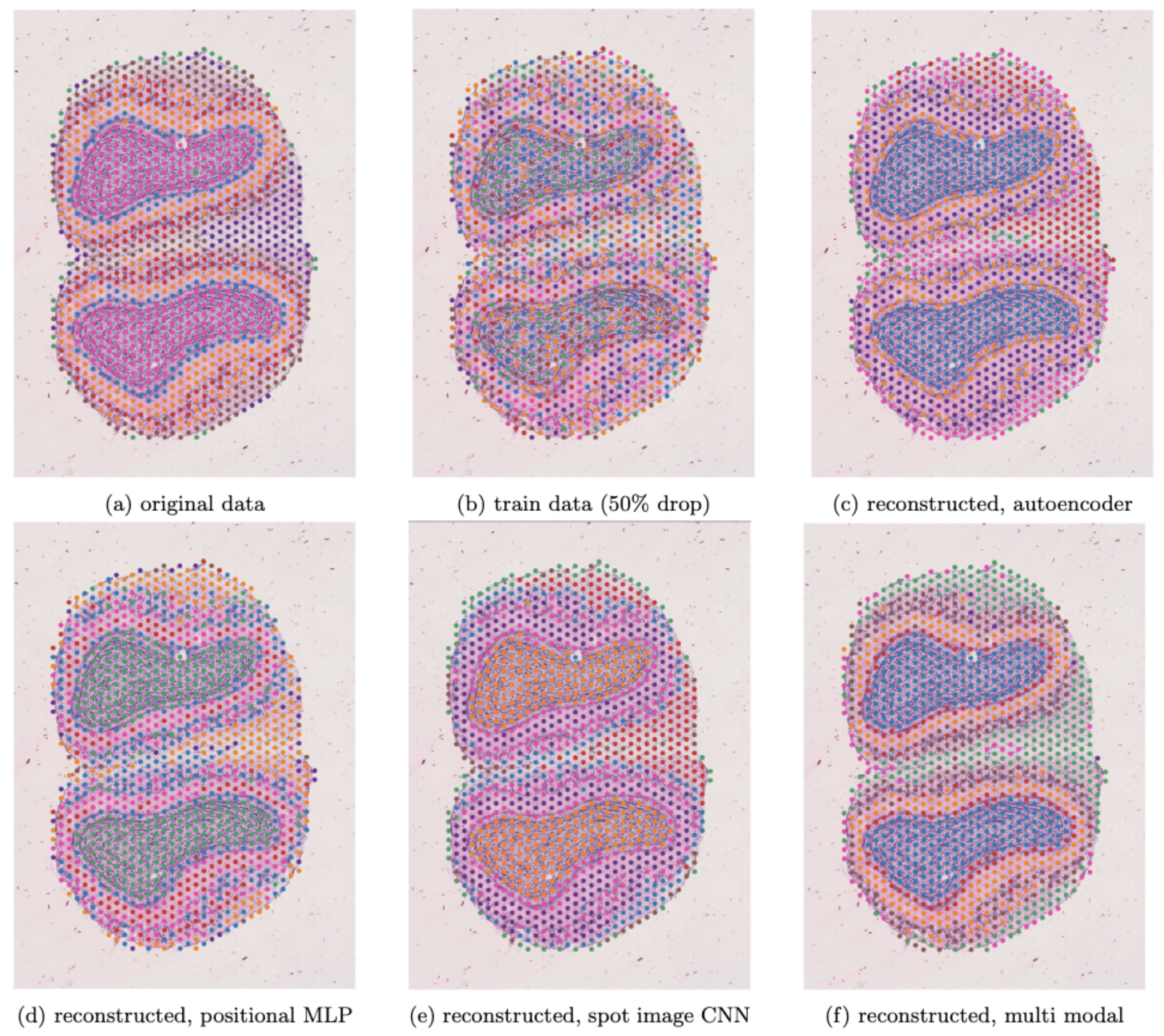
First, we drop a significant amount (~50%) of the non-zero elements in the original matrix, and reserve them as a test set. The resulting dropped matrix is then used as the training set. After training the network with the dropped matrix we can then built an imputed result matrix. We then perform both quantitative and qualitative analysis on the result.

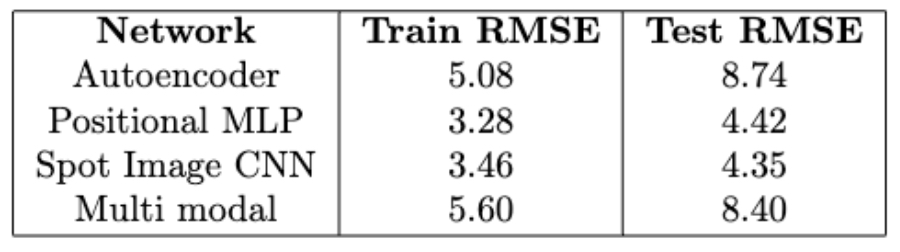
For quantitative analysis we compare the original dropped values with the same indices in the imputed matrix, and measure the RMSE. See the table below.

For qualitative analysis we perform cell-type clustering on three different matrices: the original matrix, the post-dropout training set matrix, and the imputed matrix. In successful efforts we expect to see that the resulting cluster distribution on the imputed matrix has a similar pattern as the original pre-dropout matrix. See figure below.

Discussion - summary

Viewing the quantitative results in the above table as well as the qualitative results in the above plot, we see a few points worth mentioning:

• All of the models overfit to a certain extent.
• The supervised models (positional and spot image) show better RMSE results than the autoencoder both in terms of test results and in terms of less overfitting.
• The multi modal approach achieves slightly better RMSE results than the autoencoder but less impressive results than the other networks.
• Comparing the RMSE results to the cell clustering results, however, shows us that in this case, the RMSE results can be misleading. The supervised networks show better results in terms of RMSE, and so quantitatively their reconstructed matrices are closer to the original train matrix. And yet, the underlying signal is not restored, and the cell clustering is not as correct compared to the ground truth cell clusters. In this case, the autoencoder, and even more so the final multi modal approach seem to much better restore the underlying signal and generate a more correct cluster map.